目录

数据结构:迷宫问题

waruto210 收录于数据结构

2018-11-10 约 870 字预计阅读 2 分钟

目录

设计思路

图编号

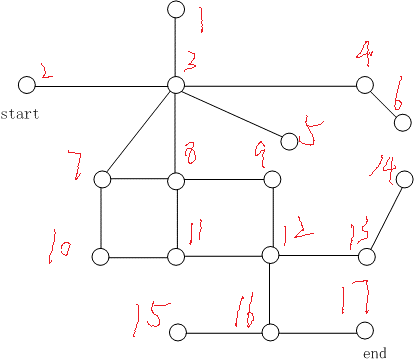
如图所示，从上到下，从左到右，给 17 个顶点进行编号，以两个顶点代表一条边，例入 2-3 代表可以从顶点 2 走到顶点 3。问题即为求解从 2 -> 17 的通路。

求解思想

求解一条通路，应当从起点出发，不断前进到后续可行顶点，当在一个顶点无法继续前进时，则回退到上一个顶点，寻找其他可行顶点，直到到达终点。此思想符合数据结构栈的特点。首先将起点压栈，然后将从当前顶点可到达的一个顶点压栈，然后将该顶点标记为已访问，随后到达下一个顶点，在某个顶点无法继续走通时，将当前顶点出栈，回退到上一个顶点重新选择可以到达的且未访问的顶点。如此循环，直到终点被压入栈中，此时栈中所有顶点即为一条通路。

求解一条最短路径，应当从起点出发，访问所有可以到达的下一级顶点。再从所有下一级顶点出发，访问所有可访问的再下一级顶点，如此循环，每一级顶点距起点距离相同。过程中记录路线。此想法符合数据结构中队列的特点。首先，将起点入队。然后将队头元素出队，将该元素可访问到的且未被访问的顶点置为已访问，然后入队，注意记录被入队节点的前一个节点。直到队列为空。最后顺着终点的前驱顶点输出即可得到路线。若有多个终点，要寻找到最近的终点出去，则将结束循环条件改为有终点入队即可。

代码说明

结构体及全局变量定义

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


typedef struct p    //表示顶点,用于寻找最短路径时记录路径
{
    int code;
    struct p* pre;  //前一个顶点
} Ver;

const int edge_cnt = 29;    //边的数量
const int ver_cnt = 17;     //顶点数量
int map[edge_cnt][2];       //记录边
int my_stack[MAX] = {0};    //数组模拟栈
int my_quque[MAX] = {0};    //数组模拟队列
int top = 0;                //栈顶指示
int front = 0, rear = 0;    //队列首位指示
bool visit[ver_cnt + 1] = {false};  //记录点是否访问过
Ver vers[ver_cnt + 1];              //每个点路径链表头结点

函数定义

1
2
3
4
5
6


void loadmaze();            //读入迷宫地图
void visited(int i);        //将点i状态置为访问过
bool isvisited(int i);      //判断点i是否访问过
bool hasway(int s);         //从点s出发是否有没去过的可行路径
void find_way(int start, int end);      //找到一条通路
void find_least(int start, int end);    //找到一条最短路径

运行结果

实验总结

本次实验，求解迷宫通路和最短通路，在不利用递归的情况下，使用模拟的栈和队列，实现了深度优先搜索和广度优先搜索。加强了对于栈和队列的理解以及使用熟练度。